论文阅读-年龄估计_SSRNet
年龄估计,也是一个颇有点意思的task。
今天来介绍一个其中的经典算法:SSRNet。
1. 前情提要
年龄估计,其实远在深度学习风行之前就已经有了一些工作了,不过多是用传统方法来做,先提取特征,再在特征上进行分类或者回归。 提取特征的方法,比如 AAM、 LBP、 Gabor 等等,得到特征后,加个 SVM/SVR/PLSR 等就做了个年龄估计模型出来~~
而由于深度学习的再次大火,自然又有众多探索如何用深度学习做年龄这个task的了,DEX 是其一,本文的 SSRNet 也是其一。
2. 庐山真面
先来张图一睹为快:
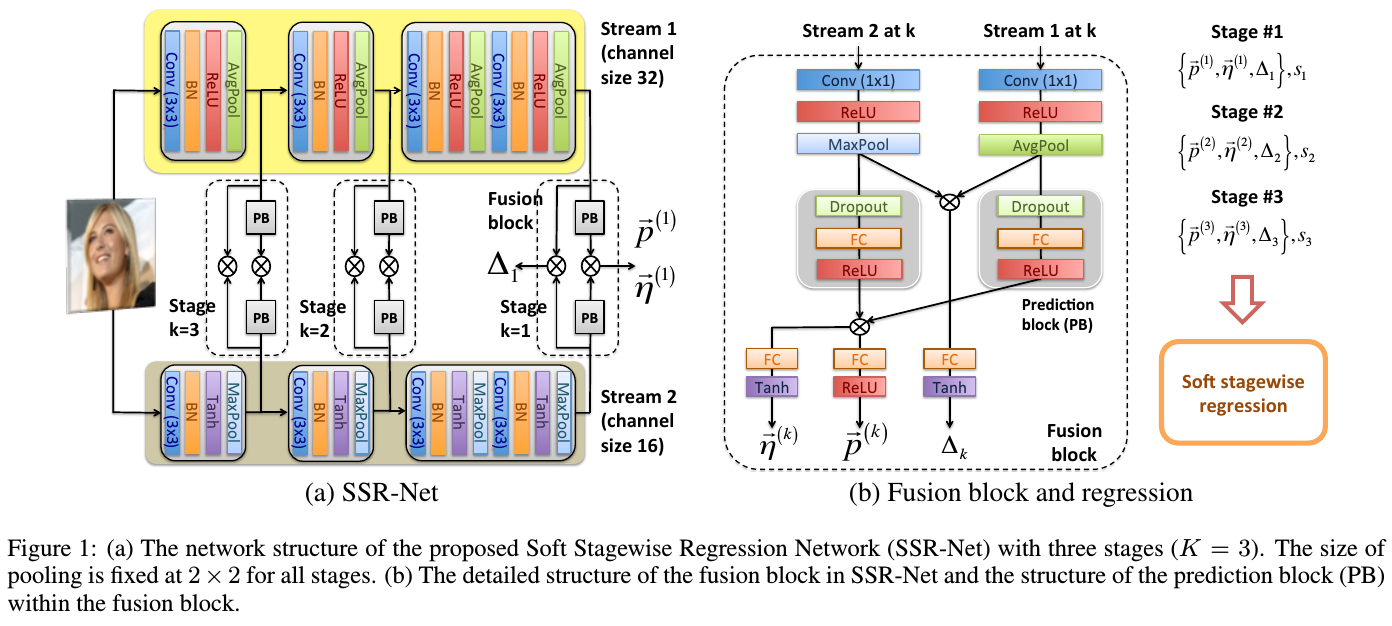
然后故事还要从 DEX 说起。
DEX 将年龄均分为 $s$ 个年龄段,即对于[0,V]的年龄跨度,每个年龄段跨度为 $V/s$,该段的代表性年龄取 $\mu = V/s$.
然后对于一个 s 类的分类模型,取其每一类的概率与当前类的代表年龄的加和作为最终的预测值:
这是 DEX 的做法。
然而,作者说:“To reduce the model size without sacrificing much accuracy, we propose to use a coarse-to-fine strategy with multi-stage prediction.”
啥意思呢,就是作者要分阶段进行 DEX 的这个操作,然后不同阶段的值再进行融合:
\[\tilde{y} =\sum_{k=1}^{K} \vec{p}^{(k)}\cdot \vec{\mu}^{(k)}=\sum_{k=1}^{K}\sum_{i=0}^{s_k-1}p_i^{(k)}\cdot i(\frac{V}{\prod_{j=1}^k s_j })\]看起来有点摸不着头脑?举个栗子:
令 V=90,也就是年龄跨度为0到90岁,阶段数 K=2,每个阶段的年龄段数为3,即$s_1=s_2=3$。 那么阶段K=1时,每段年龄分别是(0~30),(30~60),(60~90),对于阶段K=2时,每段年龄段又被 分为3段,即每段年龄分别是(+0~10),(+10~20),(+20~30)。
这么说是不是好像有点懂了?
不懂也不怕,我们先往下说,最后融会贯通,你就恍然大明白啦~~~
细心的客官应该已经发现了,上面这个式子里的$V$ 的分母变成了$\prod_{j=1}^k s_j$,这里又是作者的一个trick创新点:
作者说,年龄是连续的,而且有一定的不确定性,所以粗暴地把年龄划分为平均且不重叠的区域是不怎么flexible的,于是乎,
作者决定使用dynamic range,什么意思?就是每个年龄区域可以被shifted and scaled,怎么样,是不是觉得这个术语很面熟,当年batchnorm提出来的时候也见过对不对?
具体怎么实现这个年龄的dynamic range呢?
很简单,看:
式中,$s_k$是在阶段k时的均分不重叠的年龄区域个数,加个波动区域$\bigtriangleup_k$,则每个年龄区域的跨度应该为:
\[\bar{w}_k=\frac{V}{\prod_{j=1}^k \bar{s}_j}\]于是乎,就实现了这个scale了~~那么shift呢?
作者又把每个年龄区域的索引做了个偏移:
这样一来,每个年龄区域的索引有了微小的改变,自然也就是shift了~~
最后,就是整合各个阶段的输出来求加权和作为最终的年龄预测结果了:
\[\tilde{y}=\sum_{k=1}^{K}\sum_{i=0}^{s_k-1}p_{i}^{k}\cdot \bar{i}(\frac{V}{\prod_{j=1}^k\bar{s}_j})\]不过作者在此基础上又多走了一个trick一步:用个2-stream模型来尽量提取不同特征,融会贯通。
好了现在到了各位看官融汇贯通的时候了,现在再回头看一下开始那张图:

怎么样,是不是有种恍然大明白的感觉?
3. 顾盼生姿
最后贴张结果对比图,感性地评估一下SSRNet的性能:
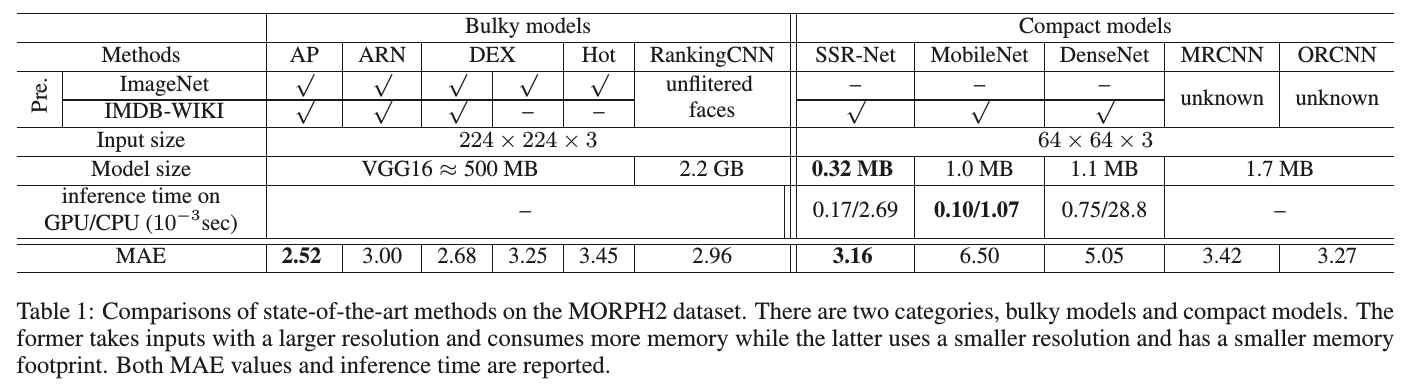
好啦, 现在到了各位看官捧个场的时候啦~~
敬请期待下次更新,完结撒花~~
微信公众号:璇珠杂俎(也可搜索oukohou),提供本站优质非技术博文~~

regards.